Hydrostatic Forces

Of the numerous forces acting on the substructure of an offshore wind turbine, amongst the most important are those due to buoyancy. It shall be assumed that the displaced fluid has density \(\rho\) [kgm \(^{-3}\)] and is within a gravity field with acceleration \(g\) [ms \(^{-2}\)].

Archmides’ Principle

This states that the magnitude of the buoyancy force \(\vec{F}_b\) is equivalent to the weight of the fluid volume that the body displaces \(V_d\). The total force can be calculated as:

\[\begin{equation} \vec{F}_b = \iint_{A} p(z)\vec{n}\,dA = \iiint_V div(p)\,dV = \rho g V_d \textrm{ , } \end{equation}\]

where \(p(z)\) is the pressure (normal stress) as a function of depth, \(\vec{n}\) is the normal to the surface and \(A\) and \(V\) are the submerged surface area and displaced volume of the body, respectively. The force acts at the centre of buoyancy, which is the centre of gravity of \(V_d\). This is shown for a simple geometry in Fig. 15.

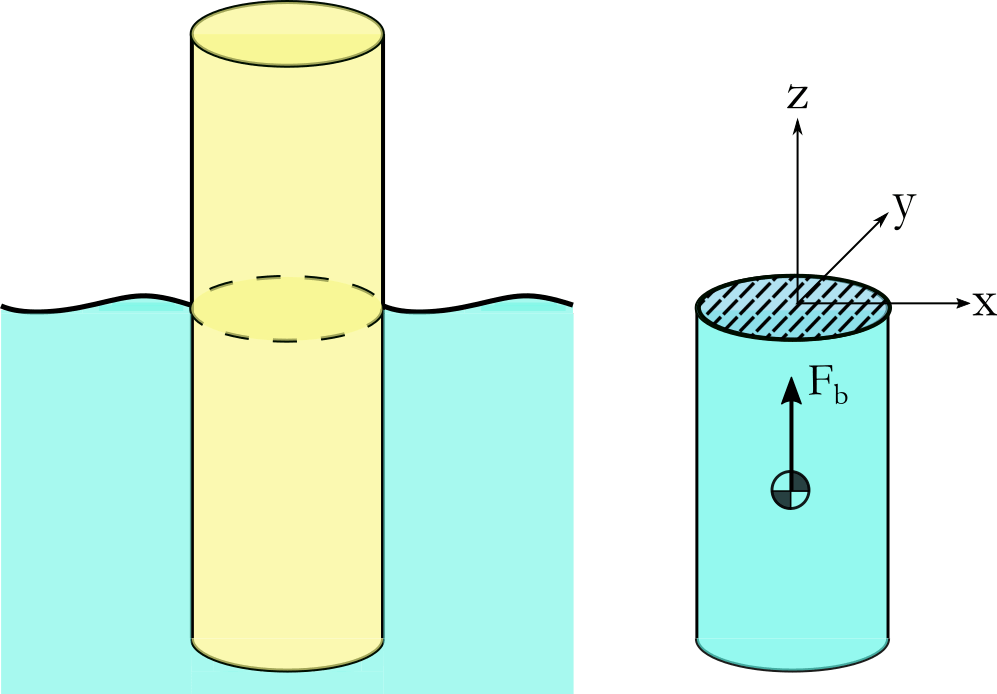
Fig. 15 Floating body (left) and the corresponding displaced volume (right).

The motion and orientation of the body and the local surface elevation causes the displaced volume to change with time, this correspondingly changes the magnitude and direction of \(\vec{F}_b\). Depending on the spatial distribution of \(V_d\), this can also induce a buoyancy moment on the body. There are three main approaches for calculating these loads.

Discrete Surface Buoyancy Calculation

In this approach the submerged surface \(A\) is discretised non-overlapping surface elements and the pressure acting over the surface is numerically integrated in order to arrive at the total buoyancy force. The hydrostatic equation is used to determine the pressure as a function of depth:

\[\begin{equation} p(z) = p_{0} - \rho g z \end{equation} \textrm{, }\]

where \(p_0\) is the atmospheric pressure at the free surface. As pressure is a normal stress, this force always acts in the direction normal to the surface \(\vec{n}\).

Discrete Volume Buoyancy Calculation

In this approach the displaced volume \(V_d\) is discretised into non-overlapping volume elements. The buoyancy force acting at the centre of buoyancy of each element are then integrated to get \(\vec{F}_b\). This is practically equivalent to the discrete surface approach, however integration is carried out over volume elements.

In QBlade the volume buoyancy calculation approach is used. In general all offshore substructures in QBlade are composed of cylindrical elements. There are two methods implemented how the buoancy of a cylinder is calculated in QBlade.

In the simple approach the intersection between the cylinder centerline and the local sea elevation is evaluated. Based on this intersection and the cylinder endpoints it is estimated wether the cylinder is not, fully or only partially submerged. The partially submerged part of the cylinder is estimated from the submerged part of the centerline. The submerged height is treated as constant around the cylinder circumference, regardless of its orientation. The buoancy force then acts on the midpoint of the submerged part of the centerline.

In the advanced buoancy approach in QBlade each cylinder is discretized into multiple prismatic elements (the element number is a user input, 100 is the suggested default value). For each of these elements the centerline approximation is carried out and then all forces are summed up and an equivalent force acting point is evaluated.

Hydrostatic Stiffness Matrix

It shall be assumed that the surface elevation is everywhere approximately constant. This can be valid if the wavelength of the sea state is much larger than the dimension of the body. Expressing the motion of the body away from the equilibrium position as a simple translation + rotation: \(d\vec{x} = [\delta_x, \delta_y, \delta_z, \theta_x , \theta_y, \theta_z]\) (surge, sway, heave, roll, pitch, yaw), the buoyancy force can be expressed as:

\[\begin{split}\begin{equation} \vec{F}_b = \vec{F}_{c} - Cd\vec{x} \hspace{5mm}\textrm{where: } \vec{F}_{c} = \begin{bmatrix} 0 \\ 0 \\ \rho g V_d \\ 0 \\ 0 \\ 0 \\ \end{bmatrix} \end{equation} \textrm{ , and: } C = \begin{bmatrix} 0 & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & C_{33}& C_{34}& C_{35}& 0 \\ 0 & 0 & C_{43}& C_{44}& C_{45}& C_{46} \\ 0 & 0 & C_{53}& C_{54}& C_{55}& C_{56} \\ 0 & 0 & 0 & 0 & 0 & 0 \\ \end{bmatrix} \textrm{. }\end{split}\]

\(\vec{F}_{c}\) is the vector representing the buoyancy force acting on the body in equilibrium. The matrix \(C\) is referred to as the hydrostatic stiffness matrix and is composed of a set of integrals over the waterplane area \(S\), shown as the hatched area in Fig. 15:

\[\begin{split}\begin{align} C_{33} & = \rho g \iint_{S} dS & C_{34} & = C_{43} = \rho g \iint_{S} y\,dS \\ C_{44} & = \rho g \iint_{S} y^2\,dS + \rho g V_d z_b & C_{35} & = C_{53} = -\rho g \iint_{S} x\,dS \\ C_{55} & = \rho g \iint_{S} x^2\,dS + \rho g V_d z_b & C_{45} & = C_{54} = -\rho g \iint_{S} xy\,dS \\ C_{46} & = -\rho g V_d x_b & C_{56} & = -\rho g V_d y_b \\ \end{align} \textrm{, }\end{split}\]

where \(\vec{B}=[x_b, y_b, z_b]\) is the deflected position of the centre of buoyancy. In practise many of these terms are zero due to symmetries of the body. It can be seen that the hydrostatic loads assume that the waterplane area does not significantly change. It is for this reason that the above expression is only valid for small rotations and translations. When the force acting on the body due to gravity is taken into account, it can be seen that the \(V_d\) terms in the \(C_{ij}\) represent restoring buoyancy moments which act to stabilise the body position. For a detailed overview of stability of floating bodies, the reader is referred to the book by Newman 1.

1

J.N. Newman. Marine Hydrodynamics. MIT Press, 2018. ISBN 9780262534826.