Multi Body Beam Formulation
The structural model in QBlade is based on the FEA module of the open source multi-physics engine Project Chrono Tasora et al.1. Project Chrono is based on a platform independent design Projectchrono.org2, which is developed in the C++ language as an object-oriented library.
For the integration into QBlade, the Chrono::Engine module is employed. Chrono::Engine is the core module of Project::Chrono, it contains functionality for setting up and solving physical systems containing Newtonian dynamics and finite elements. The SparseLU solver of the EIGEN C++ template library Tuxfamily3 is used as a solver for the finite element problem. A dynamic link library, containing the Chrono module, has been compiled from Project Chrono’s GIT repository. The relevant header files of Project Chrono and the EIGEN library are included, and the Chrono DLL is linked to QBlade’s source code. This enables the definition of the physical system and the finite elements and grants access to the solver to perform time domain simulation of structural dynamics inside QBlade.
Element and Multi-Body Formulation
The structural turbine model in the QBlade-Chrono coupling consists of Euler Bernoulli beams in a co-rotational formulation Negrut4. In the co-rotational formulation (see Fig. 16), a floating coordinate system is attached to each deformable beam element. The overall motion of a beam element is then the addition of the rigid body (translation and rotation) undergone by the floating coordinate system and a smaller strain deformation, expressed in the floating frame of reference. The global tangent stiffness matrix in Project Chrono’s implementation is formulated in a way to include terms for geometric stiffness.
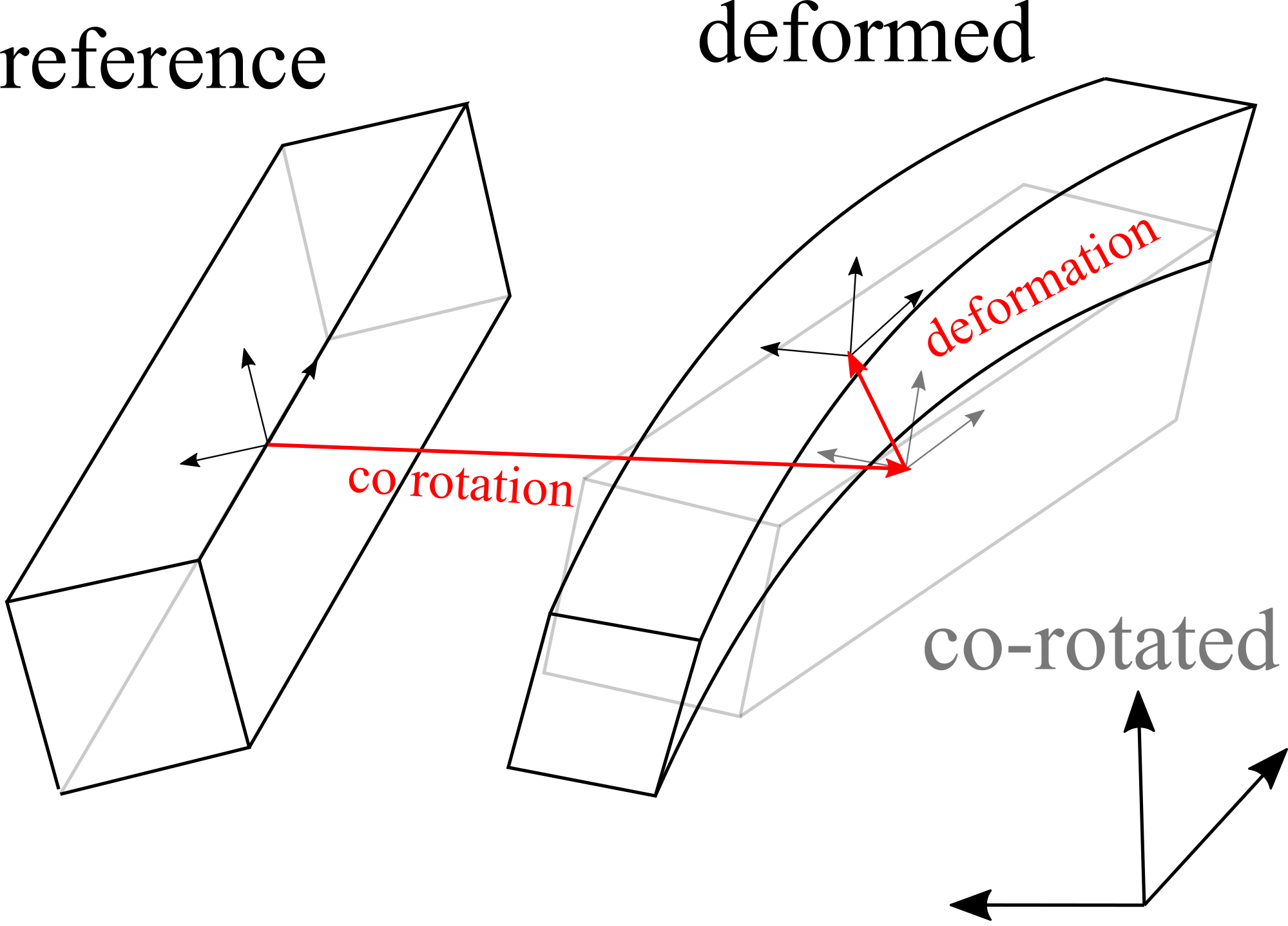
Fig. 16 Visualization of the co-rotational beam approach.
In QBlade’s implementation of the structural model, the complete turbine structure is divided up into body objects. A body object contains an array for its structural nodes, an array for its structural beam elements, a unique identifier and several functions to access forces, torques, positions, velocities, accelerations and deflections. For a common HAWT, one body is created for each blade and one body for the tower.
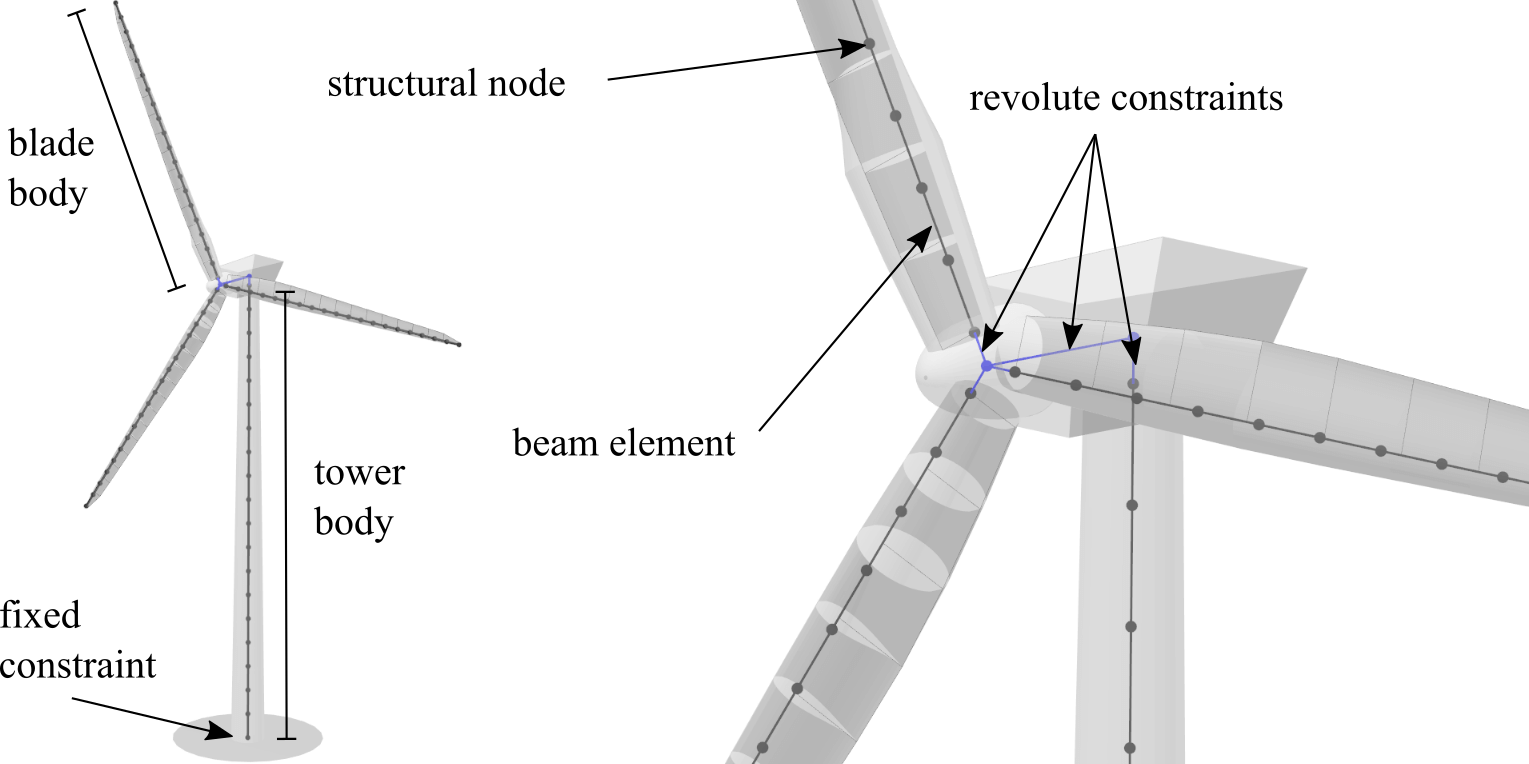
Fig. 17 Visualization of the co-rotational beam approach.
After the bodies have been created, they are assembled using joints or constraints (see Fig. 17). The tower is fixed to the ground by constraining all six DoF of the bottom tower node. A spring and damper may be defined at the ground to include foundation and soil dynamics. Using a revolute constraint, a free yaw node is connected to the tower top. Another revolute constraint then connects the hub node to the yaw node. Lastly, the blades are fixed around the hub node with revolute constraints, allowing them to rotate around the pitch axis. After the assembly of the bodies is completed, actuators are added to the revolute constraints. These actuators are used to yaw or pitch the turbine, based on controller signals and to model the generator. Actuators are implemented as engine type constraints. At these engine type constraints, either a rotational angle, a rotational speed or a torque can be applied. This functionality is used to prescribe pitch angles at the pitch constraints, yaw angles at the yaw constraint and the generator torque at the shaft constraint. Furthermore, if no controller is used within a simulation, a constant rotational speed is prescribed for the main shaft to operate the turbine at a constant rotational speed.
Time Integrators and Solver for the Structural Dynamics Simulation
Various factors influence the overall contribution of the structural model to the total computational cost of an aeroelastic simulation. The size of the problem matrix is proportional to the number of degrees of freedom that the system contains. Each main component (blades, struts, tower) of the assembled turbine can be discretized with an arbitrary number of structural nodes, where each node adds 6 degrees of freedom to the system matrix. Clearly, the total contribution of the structural model evaluations to the overall computational cost scales with the time step size of the structural evaluations. Due to the loose coupling method that is being employed in QBlade, the time step size can be set independently of that of the aerodynamic calculations.

Fig. 18 Large blade deformations caused by inertial forces during rotor ramp-up.
In the Chrono library, the multi-body FEA problem is formulated as a Differential Variational Inequality (DVI) problem. At each time step of the structural simulation, the DVI problem is solved using the EIGEN SparseLU solver, which is included in the EIGEN C++ template library Tuxfamily3. The structural simulation is then advanced using a time integrator of choice. Several different time integrators (Tasora5) are available in Chrono. However, only the iterative HHT (Hilber-Hughes-Taylor formulation) has proven its usability within the current integration of Chrono in QBlade. While other, non-iterative, integrators suffer from constraint drifts or require very small timesteps to yield reasonable results, the HHT integrator shows good performance for structural time steps in the range of up to 5 degree azimuthal rotor increments.
- 1
Alessandro Tasora, Hammad Mazhar Radu Serban2, Arman Pazouki, Daniel Melanz, Jonathan Fleischmann, Michael Taylor, Hiroyuki Sugiyama, and Dan Negrut. Chrono: An Open Source Multi-physics Dynamics Engine. Tasora, A., Serban, R., Mazhar, H., Pazouki, A., Melanz, D., Fleischmann, J., … Negrut, D. (2016). Chrono: An Open Source Multi-physics Dynamics Engine. High Performance Computing in Science and Engineering, 19–49. doi:10.1007/978-3-319-40361-8_2, 2016. doi:10.1007/978-3-319-40361-8_2.
- 2
Projectchrono.org. Project Chrono - An Open-Source Physics Engine. 2019. URL: https://projectchrono.org/about/ (visited on 2019-07-12).
- 3(1,2)
Tuxfamily. EIGEN - a C++ template library for linear algebry: matrices, vectors, numerical solvers and related algorithms. URL: http://eigen.tuxfamily.org (visited on 2019-07-12).
- 4
Dan Negrut. Co-rotational Formulation in Chrono Antonio Recuero Chrono. pages 1–10, 2016. doi:.
- 5
Alessandro Tasora. Time integration in Chrono::Engine. pages 1–44, 2017. doi:.