Blade Element Momentum Method
In QBlade the aerodynamic forces acting on a rotor can be modeled either using a steady Blade Element Momentum (BEM) or a with a more advanced, time resolved unsteady BEM (UBEM) which is enhanced by several correctional models. The theory interlinks the actuator disc theory and the blade element theory and it was first introduced by Glauert1. Despite its simplicity, the BEM method allows for an accurate representation of the steady aerodynamic loads that act on the rotor of a wind turbine, provided certain model assumptions are not violated.
Momentum Theory
Under the assumptions of a steady, incompressible and axisymmetric inflow of an inviscid fluid the actuator disc theory may be applied. The rotor plane is treated as an actuator disk that causes a uniform pressure drop over the rotor area while the flow velocity varies continuously through the disk. In its simplest form, the actuator disc theory assumes that the velocity through the rotor plane does not contain a tangential component and the pressures far up- and downstream of the rotor are equal to the ambient pressure. These assumptions allow for the calculation of the rotor performance (power and thrust) and the velocity in the rotor plane by invoking the conservation of mass and momentum (see Branlard2). The introduction of the induction factor \(a\) allows for the expression of the velocity in the rotor plane as function of the incoming velocity \(u_{0}\):
The rotor performance coefficients for power and thrust may also be expressed as a function of the axial induction factor \(a\):
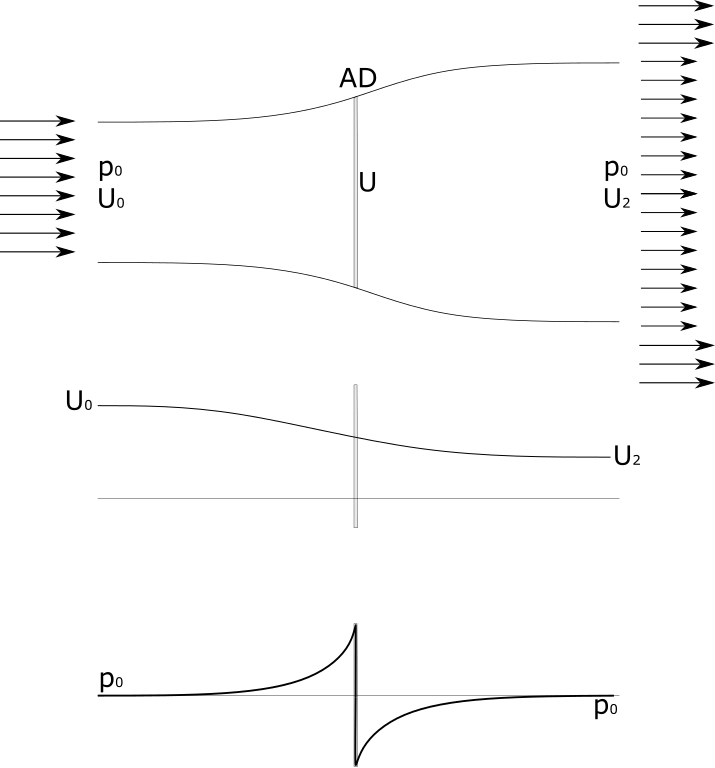
Fig. 2 1D momentum theory, pressure and velocity evolution.
Blade Element Theory
The blade element theory allows for the computation of the loads acting on a rotor based on the geometric and aerodynamic properties of individual spanwise blade sections. The blade is divided into a discrete number of radially distributed sections. The loads on each section are calculated under the assumption that the flow there is locally two-dimensional and in the plane of the airfoil section. This allows for the use of two-dimensional lift, drag and moment coefficients together with the relative flow velocity to determine sectional airfoil forces.
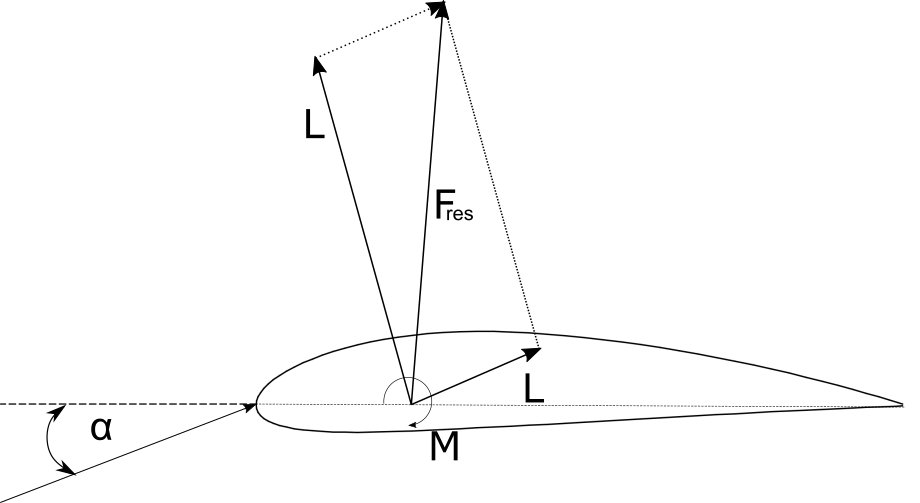
Fig. 3 2D forces on an airfoil.
Classical Blade Element Momentum Theory
The blade element momentum theory combines the 1D actuator disc theory with the blade element theory. For practical reasons, the stream tube theory is applied to radial annuli that match the discretization of the blade elements. Both theories allow for the expression of the blade forces within an annular segment as a function of streamtube geometric properties and the axial and tangential induction factors \(a\) and \(a'\), respectively. A solution method is applied which iteratively finds the values of \(a\) and \(a'\) which satisfy both theories.
Corrections
Due to the two dimensional nature of the BEM theory, three dimensional effects are not accounted for by the classical BEM. This leads to large deviations of flow quantities compared with measured turbine data, particularly in regions where strong changes in the blade circulation occur. To improve the accuracy of the BEM results, two correctional methods are implemented into QBlade:
Unsteady Blade Element Momentum Theory
Although the classical BEM method provides good estimates of the annual energy production, it is incapable of accounting for unsteady phenomena like the atmospheric boundary layer, turbulence or the tower influence. These unsteady phenomena make the position of each blade at a certain time necessary. Hence, non-rotating coordinate systems are placed at the bottom of the tower and the nacelle. Furthermore, a coordinate system is attached to the rotating shaft and each blade. The instantaneous velocity seen by each blade can now be determined and be accounted for in the calculation of the flow angle (Tavares da Silva and Donadon4). As the classical BEM is only valid for steady flow cases and provides induced velocities corresponding to this specific state, a dynamic inflow model is used to introduce a time lag to the sectional rotor induction (see Glauert1 or Henriksen et al.5).
Polar Grid
The polar-grid has been developed by (Madsen et al.6) to consider azimuthal variations of the axial induction caused by the azimuthal dependence of blade loadings. Within the approach, the annular rings of the actuator disc theory are divided into stationary azimuthal sections. Each point on the azimuthal grid is associated with a local induction factor, based on the local instantaneous velocity. The latter is approximated by the induced velocity of the neighboring two blades and weighted by their azimuthal distance (Behrens de Luna et al.7).
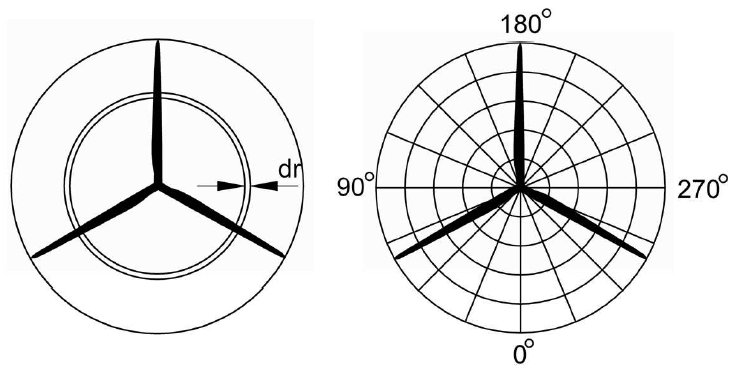
Fig. 4 Classical BEM approach (left) and polar grid with azimuthal sub elements (right), taken from Madsen et al.6)
- 1(1,2,3)
H. Glauert. Airplane Propellers, chapter Aerodynamic Theory, pages 169–360. Springer Berlin Heidelberg, 1935. doi:10.1007/978-3-642-91487-4_3.
- 2
Emmanuel Branlard. Wind Turbine Aerodynamics and Vorticity-Based Methods. Volume 7. Springer International Publishing AG, 01 2017. ISBN 978-3-319-55163-0. doi:10.1007/978-3-319-55164-7.
- 3
H. Snel, R. Houwink, W. J. Piers. Sectional Prediction of 3D Effects for Separated Flow on Rotating Blades. In Proc. European Community Wind Energy Conference. Lübeck - Travemünde, 1992.
- 4
Claudio Tavares da Silva and Mauricio Donadon. Unsteady blade element-momentum method including returning wake effects. Journal of Aerospace Technology and Management, 5:, 03 2013. doi:10.5028/jatm.v5i1.163.
- 5
L.C. Henriksen, M.H. Hansen, and Niels Poulsen. A simplified dynamic inflow model and its effect on the performance of free mean wind speed estimation. Wind Energy, 16:, 09 2012. doi:10.1002/we.1548.
- 6(1,2)
Helge Madsen, Torben Larsen, Georg Pirrung, Ang Li, and Frederik Zahle. Implementation of the blade element momentum model on a polar grid and its aeroelastic load impact. Wind Energy Science, 5:1–27, 01 2020. doi:10.5194/wes-5-1-2020.
- 7
R. Behrens de Luna, D. Marten, T. , Barlas, S.G. Horcas, N. Ramos-Garcia, A. Li, and C.O. Paschereit. Comparison of different fidelity aerodynamic solvers on the IEA 10MW turbine including novel tip extension geometries, Journal of Physics Conference Series [accepted]. Journal of Physics: Conference Series, 2022.